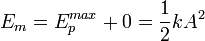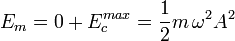DINAMICA DEL MOVIMIENTO ARMONICO

DINÁMICA DEL MOVIMIENTO ARMÓNICO SIMPLE

Un movimiento armónico simple es el que describe una partícula sometida a una fuerza restauradora proporcional a su desplazamiento. Se genera entonces un movimiento periódico, es decir que se repite cada cierto intervalo de tiempo. No todos los movimientos periódicos son armónicos. Para que lo sean, la fuerza restauradora debe ser proporcional al desplazamiento.

El problema del oscilador armónico simple aparece con mucha frecuencia en Física, ya que una masa en equilibrio bajo la acción de cualquier fuerza conservativa, en el límite de movimientos pequeños, se comporta como un oscilador armónico simple.

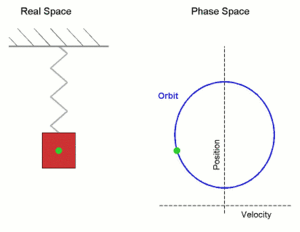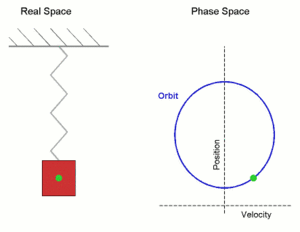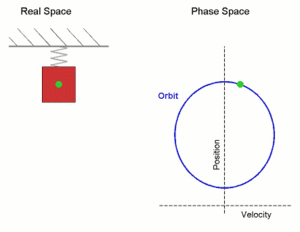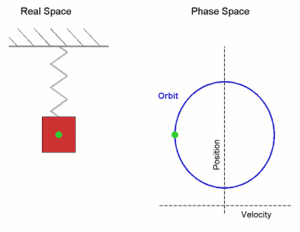
En la siguiente animación se muestra el movimiento de una masa sujeta a un muelle. Pinchando sobre ella y arrastrando se desplaza de su posición de equilibrio. Con el mando puedes variar su frecuencia de oscilación.

A continuación se explica el movimiento que describe la masa bajo la acción de la fuerza recuperadora del muelle.

                     

La masa sujeta al muelle describe un movimiento oscilatorio. Para calcular su aceleración utilizamos la Segunda Ley de Newton:

Definimos la frecuencia angular ω como:

Sus unidades en el SI son rad/s.

Posición, velocidad y aceleración

Para calcular la posición de la masa en función del tiempo habría que resolver la ecuación diferencial anterior que relaciona la aceleración con el desplazamiento.

Sin embargo, para simplificar vamos a dar la solución. Derivándola dos veces se demuestra fácilmente que satisface la Segunda Ley de Newton.

La constante A que aparece en la expresión anterior se denomina amplitud del movimiento, y es el máximo desplazamiento de la masa con respecto a su posición de equilibrio x = 0. Sus unidades en el SI son los metros (m).

El argumento del coseno es la fase y se mide en radianes.

δ es la constante de fase y viene determinada por las condiciones iniciales del problema.

El tiempo que tarda la masa en efectuar una oscilación completa se denominaperiodo (T), y está relacionado con la frecuencia angular mediante la expresión:

El número de oscilaciones que se realiza en un segundo se llama frecuencia ν y se calcula como la inversa del periodo:

Se mide en s^-1 o Herzios (Hz)

De la definición de frecuencia se obtiene que 

La velocidad y la aceleración de una partícula que describe un movimiento armónico simple se obtiene derivando la ecuación de la posición en función del tiempo.

Posición, velocidad y aceleración de una partícula que describe un movimiento armónico simple. La fase en este caso es cero.

Energía

Si no existe rozamiento entre el suelo y la masa, la energía mecánica de esta última se conserva. Ya se vio en el apartado de trabajo que la fuerza recuperadora del muelle es una fuerza conservativa y se calculó su energía potencial asociada, que es una parábola:

En la siguiente figura se ha representado la energía total, la energía potencial elástica y la cinética para distintas posiciones de una partícula que describe un movimiento armónico simple.

La energía mecánica se conserva, por lo que para cualquier valor de x la suma de la energía cinética y potencial debe ser siempre:

.

MOVIMIENTO ARMONICO FORMULAS

Fórmulas de Movimiento Armónico Simple M.A.S.: Cinemática, dinámica y energía 

Ecuación de posición

	x → Seno	x → Coseno
Con $\omega$	$$x=A·\sin \left(\omega ·t+{\phi }_0\right)$$	$$x=A·\cos \left(\omega ·t+\phi {\text{'}}_0\right)$$
Con f	$$x=A·\sin \left(2·\mathrm{\pi }·f·t+{\phi }_0\right)$$	$$x=A·\cos \left(2·\mathrm{\pi }·f·t+\phi {\text{'}}_0\right)$$
Con T	$$x=A·\sin \left(\frac{2·\mathrm{\pi }}{\mathrm{T}}·t+{\phi }_0\right)$$	$$x=A·\cos \left(\frac{2·\mathrm{\pi }}{T}·t+\phi {\text{'}}_0\right)$$

Donde:

• A: Amplitud máxima del movimiento. Representa la distancia máxima a la posición de equilibrio. Su unidad de medida en el Sistema Internacional es el metro (m)
• f: Frecuencia del movimiento. Es el número de oscilaciones o vibraciones que se producen en un segundo. Su unidad de medida en el Sistema Internacional es el Hertzio (Hz). 1 Hz = 1 oscilación /segundo = 1 s-1.
• T: Periodo del movimiento. El tiempo que tarda en cumplirse una oscilación completa. Es la inversa de la frecuencia T = 1/f . Su unidad de medida en el Sistema Internacional es el segundo (s).
• $\omega$ : Frecuencia angular o pulsación. Representa el número de periodos comprendidos en 2·π segundos. Su unidad de medida en el sistema internacional es el radián por segundo ( rad/s ). Se encuentra relacionada con la frecuencia y el periodo del movimiento según $\omega =\frac{2·\pi }{T}=2·\pi ·f$  
• ${\phi }_0$  y $\phi {\text{'}}_0$ : Fase inicial. Se trata del ángulo que representa el estado inicial de vibración, es decir, la posición x del cuerpo en el instante t = 0. Su valor depende de si has elegido un seno o un coseno para representar el movimiento. $\phi {\text{'}}_0={\phi }_0-\pi /2$ Su unidad de medida en el Sistema Internacional es el radián (rad) .

Para cualquier instante t se cumple que $x\left(t\right)=x(t+T)$ .

Gráfica de posición x - t

La velocidad es máxima cuando el cuerpo pasa por la posición de equilibrio y mínima en los extremos de latrayectoria del movimiento (+A y -A).

MOVIMIENTO SIMPLE

El movimiento armónico simple (m.a.s.), también denominado movimiento vibratorio armónico simple(m.v.a.s.), es un movimiento periódico, y vibratorio en ausencia de fricción, producido por la acción de una fuerza recuperadora que es directamente proporcional a la posición, y que queda descrito en función del tiempopor una función senoidal (seno o coseno). Si la descripción de un movimiento requiriese más de una función armónica, en general sería un movimiento armónico, pero no un m.a.s.

En el caso de que la trayectoria sea rectilínea, la partícula que realiza un m.a.s. oscila alejándose y acercándose de un punto, situado en el centro de su trayectoria, de tal manera que su posición en función deltiempo con respecto a ese punto es una sinusoide. En este movimiento, la fuerza que actúa sobre la partícula es proporcional a su desplazamiento respecto a dicho punto y dirigida hacia éste.

ENERGÍA DEL MOVIMIENTO ARMÓNICO SIMPLE

Las fuerzas involucradas en un movimiento armónico simple son centrales y, por tanto, conservativas. En consecuencia, se puede definir un campo escalar llamado energía potencial (E_p) asociado a la fuerza. Para hallar la expresión de la energía potencial, basta con integrar la expresión de la fuerza (esto es extensible a todas las fuerzas conservativas) y cambiarla de signo, obteniéndose:

(15)

La energía potencial alcanza su máximo en los extremos de la trayectoria y tiene valor nulo (cero) en el punto x= 0, es decir el punto de equilibrio.

La energía cinética cambiará a lo largo de las oscilaciones pues lo hace la velocidad:

(16)

La energía cinética es nula en -A o +A (v=0) y el valor máximo se alcanza en el punto de equilibrio (máxima velocidad Aω).

(17)

Como sólo actúan fuerzas conservativas, la energía mecánica (suma de la energía cinética y potencial) permanece constante.

(18)

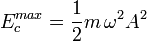
Finalmente, al ser la energía mecánica constante, puede calcularse fácilmente considerando los casos en los que la velocidad de la partícula es nula y por lo tanto la energía potencial es máxima, es decir, en los puntos  y . Se obtiene entonces que,

(19)

O también cuando la velocidad de la partícula es máxima y la energía potencial nula, en el punto de equilibrio 

(20)