El movimiento armónico simple (m.a.s.), también denominado movimiento vibratorio armónico simple(m.v.a.s.), es un movimiento periódico, y vibratorio en ausencia de fricción, producido por la acción de una fuerza recuperadora que es directamente proporcional a la posición, y que queda descrito en función del tiempopor una función senoidal (seno o coseno). Si la descripción de un movimiento requiriese más de una función armónica, en general sería un movimiento armónico, pero no un m.a.s.
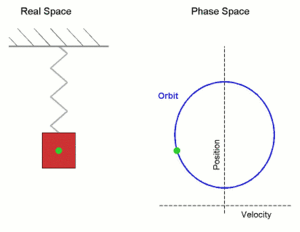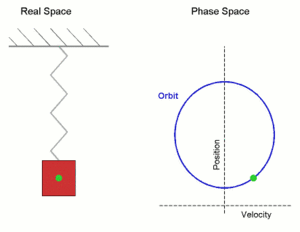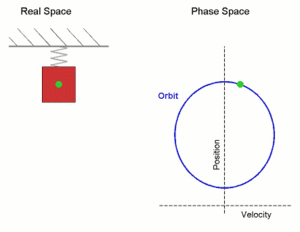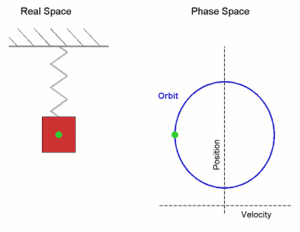
En el caso de que la trayectoria sea rectilínea, la partícula que realiza un m.a.s. oscila alejándose y acercándose de un punto, situado en el centro de su trayectoria, de tal manera que su posición en función deltiempo con respecto a ese punto es una sinusoide. En este movimiento, la fuerza que actúa sobre la partícula es proporcional a su desplazamiento respecto a dicho punto y dirigida hacia éste.
ENERGÍA DEL MOVIMIENTO ARMÓNICO SIMPLE
Las fuerzas involucradas en un movimiento armónico simple son centrales y, por tanto, conservativas. En consecuencia, se puede definir un campo escalar llamado energía potencial (Ep) asociado a la fuerza. Para hallar la expresión de la energía potencial, basta con integrar la expresión de la fuerza (esto es extensible a todas las fuerzas conservativas) y cambiarla de signo, obteniéndose:
(15)
La energía potencial alcanza su máximo en los extremos de la trayectoria y tiene valor nulo (cero) en el punto x= 0, es decir el punto de equilibrio.
La energía cinética cambiará a lo largo de las oscilaciones pues lo hace la velocidad:
(16)
La energía cinética es nula en -A o +A (v=0) y el valor máximo se alcanza en el punto de equilibrio (máxima velocidad Aω).
(17)
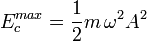
Como sólo actúan fuerzas conservativas, la energía mecánica (suma de la energía cinética y potencial) permanece constante.
(18)
Finalmente, al ser la energía mecánica constante, puede calcularse fácilmente considerando los casos en los que la velocidad de la partícula es nula y por lo tanto la energía potencial es máxima, es decir, en los puntos 
y 
. Se obtiene entonces que,
(19)
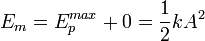
O también cuando la velocidad de la partícula es máxima y la energía potencial nula, en el punto de equilibrio 
(20)
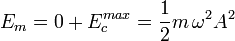
ENERGÍA DEL MOVIMIENTO ARMÓNICO SIMPLE
Las fuerzas involucradas en un movimiento armónico simple son centrales y, por tanto, conservativas. En consecuencia, se puede definir un campo escalar llamado energía potencial (Ep) asociado a la fuerza. Para hallar la expresión de la energía potencial, basta con integrar la expresión de la fuerza (esto es extensible a todas las fuerzas conservativas) y cambiarla de signo, obteniéndose:
(15)
La energía potencial alcanza su máximo en los extremos de la trayectoria y tiene valor nulo (cero) en el punto x= 0, es decir el punto de equilibrio.
La energía cinética cambiará a lo largo de las oscilaciones pues lo hace la velocidad:
(16)
La energía cinética es nula en -A o +A (v=0) y el valor máximo se alcanza en el punto de equilibrio (máxima velocidad Aω).
(17)
Como sólo actúan fuerzas conservativas, la energía mecánica (suma de la energía cinética y potencial) permanece constante.
(18)
Finalmente, al ser la energía mecánica constante, puede calcularse fácilmente considerando los casos en los que la velocidad de la partícula es nula y por lo tanto la energía potencial es máxima, es decir, en los puntos y . Se obtiene entonces que,
y . Se obtiene entonces que,(19)
O también cuando la velocidad de la partícula es máxima y la energía potencial nula, en el punto de equilibrio
(20)
No hay comentarios:
Publicar un comentario